Τι είναι η “θεωρία των παιγνίων” στην οποία ειδικεύεται ο κ. Γιάνης Βαρουφάκης. Ο Τζον Νας, που ανέπτυξε τη μεθοδολογία της, είναι το θέμα της ταινίας: “Ένας υπέροχος άνθρωπος”. Το διάσημο δίλημμα του φυλακισμένου.

Η «θεωρία των παιγνίων» είναι μια μεθοδολογία η οποία χρησιμοποιείται, μεταξύ άλλων και στη σύγχρονη οικονομία και μελετά τη συμπεριφορά των «παικτών» που ακολουθούν μια στρατηγική αλληλεπίδρασης. Φυσικά ο παίκτης μπορεί να είναι μια επιχείρηση, ένα κράτος, μια ομάδα ή ένα κόμμα και μια κυβέρνηση.

Εφαρμόζεται κυρίως για τη λήψη αποφάσεων για στρατηγικές συμμαχίες και το κύριο χαρακτηριστικό της είναι ότι κάθε «παίκτης» αλληλεπιδρά με τον/τους υπόλοιπους.

Πολύ απλά οι αποφάσεις και οι επιλογές του παίκτη, εξαρτώνται από τις αποφάσεις και τις επιλογές των υπολοίπων.

Οι παίκτες δεν είναι υποχρεωτικά «αντίπαλοι» μεταξύ τους, αλλά μπορεί να είναι και συνεργάτες, που έχουν όμως σαν σκοπό να πετύχουν το καλύτερο δυνατό αποτέλεσμα ο καθένας για τον εαυτό του ή την ομάδα του.

Η θεωρία των παιγνίων εφαρμόζεται στην πολιτική, την οικονομία, την ψυχολογία, τις πολιτικές επιστήμες, τη διοίκηση επιχειρήσεων και σε άλλους κλάδους, όταν πρέπει να χαραχθεί μια πολιτική ή μια στρατηγική.

Το πιο απλοποιημένο παράδειγμα της θεωρίας είναι «η μάχη των φύλων», όπου παίκτες είναι ένας άντρας (Α) και μια γυναίκα (Γ) και η απόφαση που πρέπει να ληφθεί είναι το πώς θα περάσουν το βράδυ τους.

Ο Α θέλει να πάνε στο γήπεδο να παρακολουθήσουν έναν αγώνα ποδοσφαίρου (Π) και η Γ θέλει να πάνε στο θέατρο να παρακολουθήσουν μια θεατρική παράσταση (Θ) και κανείς από τους δύο δεν θέλει να μείνει μόνος του.

Το καλύτερο δυνατό αποτέλεσμα για τον καθένα έχει άμεση σχέση με τις επιλογές και τις αποφάσεις του άλλου.

Οι ωφέλειες του κάθε παίκτη, απεικονίζονται στον παρακάτω πίνακα:

Α,Γ	Π	Θ
Π	2,1	0,0
Θ	0,0	1,2

Το ξεκίνημα της θεωρίας

Η βάση της θεωρίας ξεκίνησε το 1928 από τον μαθηματικό Τζον Βον Νιούμαν, ο οποίος διατύπωσε το θεώρημα του «μηδενικού αθροίσματος».

Σύμφωνα με αυτό, η ζημιά ενός παίκτη ισορροπείται και είναι ίση με το κέρδος ενός άλλου.

Ο ουγγρικής καταγωγής μαθηματικός συνέχισε να μελετά τη θεωρία του σε συνεργασία με τον Όσκαρ Μόργκεστερν και το 1944 τη δημοσίευσε με τον επίσημο τίτλο «Θεωρία παιγνίων και οικονομικής συμπεριφοράς».

Τη δεκαετία του ’50 ο μαθηματικός Τζον Νας, η ζωή του οποίου αποτελεί το θέμα της ταινίας «Ένας υπέροχος άνθρωπος», ανέπτυξε τη μεθοδολογία του για τη θεωρία των παιγνίων.

Σύμφωνα με τον Έλληνα ερευνητή Νίκο Λυγερό: «Ο Τζον Νας έδειξε ότι σε κάθε στατικό παιχνίδι με ένα πεπερασμένο σύνολο στρατηγικών, υπάρχει τουλάχιστον μια κατάσταση ισορροπίας, που αντιστοιχεί σε επιλογές στρατηγικής, οι οποίες παρέχουν τη βέλτιστη ανταπόδοση και για τους δύο παίκτες. Κανένας παίκτης δεν μπορεί να πετύχει κάτι καλύτερο αλλάζοντας τη στρατηγική του, τη στιγμή που η στρατηγική του άλλου παραμένει αμετάβλητη.

Η εργασία του Νας δεν δείχνει ωστόσο το πως μπορεί κανείς να υπολογίσει μια τέτοια ισορροπία  ούτε πόσες από αυτές υπάρχουν.

Στη πραγματικότητα, ακόμη και απλά παιχνίδια έχουν μια πλειάδα ισορροπιών Νας και δεν υπάρχει τρόπος να ξεχωρίσει κάποια ιδιαίτερη.

Μάλιστα εκτός από το γεγονός, ότι αν και οι δύο παίκτες αποφασίσουν να μεγιστοποιήσουν την ανταπόδοσή τους, υπάρχει περίπτωση να καταλήξουν στο χειρότερο δυνατό αποτέλεσμα και για τους δύο.

Το πρόσθετο πρόβλημα είναι πως ακόμη και αν διαλέξουν μια στρατηγική που αντιστοιχεί σε μια ισορροπία Νας, το αποτέλεσμα μπορεί να είναι να απεμπολήσουν μια ευνοϊκότερη ανταπόδοση».

Το δίλημμα του φυλακισμένου

Το πιο γνωστό δίλημμα για τη θεωρία των παιγνίων είναι το δίλημμα του φυλακισμένου».

Η μαθηματικός Βικτώρια Πολύζου το εξηγεί σε άρθρο της: “Η ονομασία “δίλημμα του φυλακισμένου” έχει δοθεί σε ένα τύπο παιχνιδιού, μη μηδενικού αθροίσματος που επινόησαν, το 1950, ο Μ.Flood και M. Dresdher, εργαζόμενοι στην RAND Cor. και το οποίο ο  A.Tucker απευθυνόμενος σε ψυχολόγους, το παρουσιάζει χρησιμοποιώντας ένα παράδειγμα με φυλακισμένους και ποινές για λόγους κατανόησης. Αυτό είναι ένα από τα πιο διάσημα προβλήματα της θεωρίας παιγνίων.

Πρόκειται για ένα απλό παράδειγμα που εφαρμόζεται σε πολλές καταστάσεις όπου οι δύο δυνάμεις έρχονται σε αντιπαράθεση και μπορούν να επιλέξουν ανάμεσα στη σύγκρουση ή την συνεργασία πχ σ΄ ένα πόλεμο τιμών, μια διαφημιστική εκστρατεία ή ακόμη τον ανταγωνισμό πολεμικών εξοπλισμών.

Το δίλημμα έχει ως εξής:

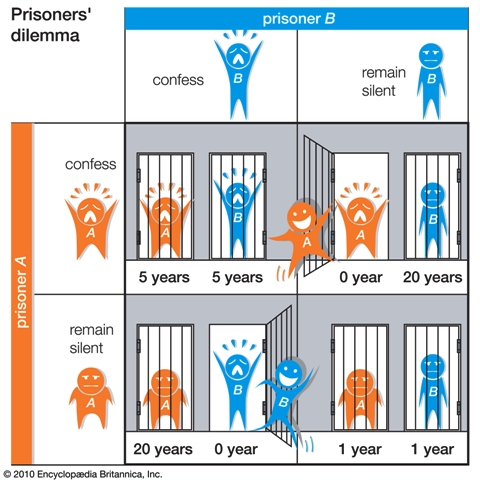Δύο άνθρωποι (εμείς θα τους αποκαλούμε Α και Β) είναι ύποπτοι για την τέλεση ενός εγκλήματος. Όμως η αστυνομία δεν έχει επαρκή στοιχεία για την ενοχή τους. Ο ανακριτής καλεί τον Α στο γραφείο του και του λέει τα εξής:

Αν επιρρίψει την ευθύνη στον Β και ο Β δεν μιλήσει θα αφεθεί ελεύθερος, ενώ ο Β θα κάνει 10 χρόνια φυλακή.

Αν όμως και ο Β επιρρίψει την ευθύνη στον Α και οι δύο θα   φυλακιστούν για 4 χρόνια.

Αν δεν μιλήσει και τον κατηγορήσει  ο Β, οι όροι αντιστρέφονται. Ο Β θα αφεθεί ελεύθερος και ο Α θα μείνει στη φυλακή για 10 χρόνια.

Αν όμως και οι δυο δεν ομολογήσουν θα φυλακιστούν μόνο για ένα χρόνο, λόγω έλλειψης στοιχείων.

Την ίδια συζήτηση κάνει και με τον Β.

Ο Α και ο Β δεν συναντιούνται και δεν επικοινωνούν μεταξύ τους.

Ας έρθουμε λοιπόν στη θέση του Παίκτη Β. Σκέπτεται: “Αν ο Α με έχει καρφώσει, εμένα με συμφέρει να τον καρφώσω γιατί αν το κάνω θα φάω 4 χρόνια, ενώ αν δεν το κάνω θα κάτσω στη στενή 10 χρόνια. Αν δεν με έχει καρφώσει, πάλι με συμφέρει να τον καρφώσω, γιατί θα αφεθώ ελεύθερος, ενώ αν δεν το κάνω θα κάτσω ένα χρόνο στη φυλακή. Άρα ό,τι και να κάνει ο Α εμένα με συμφέρει να τον καρφώσω”.

Φωνάζει τον δεσμοφύλακα και του λέει ότι θα ομολογήσει και θα ρίξει την ευθύνη στον Α. Όμως και ο Α σκέφτεται με τον ίδιο τρόπο και τον καρφώνει. Συνεπώς και οι δύο φίλοι μας θα κάτσουν 4 χρόνια στη φυλακή.

Ήταν όμως λογική η επιλογή τους; Αν σκεφτούμε ότι και οι δύο σκέφτηκαν το συμφέρον τους, ναι. Και οι δύο έλπιζαν ότι ο άλλος δεν θα μιλούσε και θα αφήνονταν ελεύθεροι. Τα ήθελαν όλα για τον εαυτό τους. Να κερδίσουν όσο μπορούν περισσότερα ή έστω να υποστούν όσο το δυνατόν λιγότερη ζημιά. Να όμως που ο εγωισμός τους δεν έφερε το καλύτερο αποτέλεσμα και για τους δύο, δηλαδή να μην καρφώσει ο ένας τον άλλο και να τη γλιτώσουν φτηνά με ένα χρόνο φυλάκισης ο καθένας.

Το Δίλημμα του Φυλακισμένου έγινε ευρέως γνωστό στους επιστημονικούς κύκλους και απασχόλησε επιστήμονες από πολλούς και διαφορετικούς επιστημονικούς κλάδους. Οι οικονομολόγοι είδαν στα πρόσωπα των δύο φυλακισμένων τον homο economicus, τον άνθρωπο που συμπεριφέρεται έτσι ώστε να μεγιστοποιήσει το κέρδος και να ελαχιστοποιήσει το κόστος. Οι φιλόσοφοι ασχολήθηκαν με τα ηθικά διλήμματα των παικτών. Το δίλημμα του φυλακισμένου έχει εφαρμογές στο δίκαιο, την ψυχολογία, ακόμα και τη βιολογία. Πολύ εντυπωσιακό για ένα απλό μαθηματικό παίγνιο.

Το δίλημμα του φυλακισμένου έχει εφαρμογές στο δίκαιο, την ψυχολογία, ακόμη και την βιολογία.

Υποστηρικτής και μελετητής της θεωρίας των παιγνίων, είναι ο πρώην υπουργός οικονομικών Γιάνης Βαρουφάκης, ο οποίος έχει γράψει και βιβλίο (με ομώνυμο τίτλο) για αυτή.

Σύμφωνα με τον Βαρουφάκη: Η Θεωρία Παιγνίων, αφού καταξιώθηκε ως η σύγχρονη θεμελίωση της οικονομικής, φιλοδοξεί πλέον να ενοποιήσει όλες τις κοινωνικές επιστήμες. Από τα μικρά προβλήματα της κοινωνίας (π.χ. το σχεδιασμό δημοπρασιών) μέχρι τα μεγάλα φιλοσοφικά μας αινίγματα (π.χ. περί Ηθικής και του ρόλου του Κράτους), η Θεωρία Παιγνίων έχει άποψη. Εντάσσει τον εαυτό της στα φαινόμενα που καλείται η ίδια να εξηγήσει. Αντίθετα με τις άλλες προσεγγίσεις στην κοινωνική επιστήμη, η Θεωρία Παιγνίων υποθέτει ότι κανείς δεν κάνει πράγματα που δεν θα έκανε αν τη γνώριζε! Οι κοινοί άνθρωποι εμφανίζονται σ’ αυτήν ως θεωρητικοί και οι θεωρητικοί ως κοινοί άνθρωποι. Πρωτότυπο. Όμορφο. Ανθρωπιστικό. Μήπως όμως και αυθάδες;

Διαβάστε επίσης: «Σκέφτομαι, άρα υπάρχω». Η διατύπωση του Καρτέσιου που ξεχώρισε την ύλη από το πνεύμα. Ο κατάσκοπος που ώθησε την επιστήμη και καθιέρωσε τους όρους χ, ψ, ζ, α, β, γ στην Άλγεβρα.