του αναγνώστη μας, μαθηματικού και συγγραφέα, Θανάση Κοπάδη
Η βασίλισσα είναι το πιο δυνατό πιόνι σε μια σκακιέρα, αφού μπορεί να μετακινηθεί κάθετα, οριζόντια ή διαγώνια, όσα τετράγωνα επιθυμεί.
Το πρόβλημα των 8 Βασιλισσών είναι ένα από τα πιο διαδεδομένα παιχνίδια προγραμματισμού, το οποίο μπορεί να βρει κανείς και στο Φωτόδεντρο, το Πανελλήνιο Αποθετήριο Μαθησιακών Αντικειμένων για την πρωτοβάθμια και τη δευτεροβάθμια εκπαίδευση.
Με το συγκεκριμένο πρόβλημα μπορούν να ασχοληθούν μαθητές της Γ Λυκείου, οι οποίοι καλούνται να τοποθετήσουν 8 βασίλισσες σε μια σκακιέρα 8×8 με τέτοιο τρόπο, ώστε καμία βασίλισσα να μην απειλείται από την άλλη.
Αφού εντοπίσουν τις αντικειμενικές δυσκολίες της λύσης, οι μαθητές χρησιμοποιούν προγραμματιστικό περιβάλλον για να κατασκευάσουν μια έξυπνη σκακιέρα που θα τους απαλλάξει από την προσπάθεια ελέγχου της ορθότητας της λύσης που θα αντιμετώπιζαν αν προσπαθούσαν να λύσουν το πρόβλημα σε μια πραγματική σκακιέρα.
Το συγκεκριμένο πρόβλημα αποτελεί ένα από τα βασικά μαθήματα εισαγωγής στην τεχνητή νοημοσύνη, με τις πιθανές τοποθετήσεις των 8 βασιλισσών σε μια σκακιέρα 8×8 να είναι 4.426.165.368, ενώ με τον περιορισμό ότι τοποθετούμε μια βασίλισσα ανά γραμμή οι πιθανές τοποθετήσεις πέφτουν στον αριθμό 16.777.216 και αποδεικνύεται ότι το πρόβλημα έχει 92 διαφορετικές λύσεις.
Τι γίνεται όμως αν θέλουμε να τοποθετήσουμε ένα μεγαλύτερο αριθμό από βασίλισσες, όπως για παράδειγμα 1000 βασίλισσες σε μια τετράγωνη σκακιέρα 1000×1000;
Η αρχική έκδοση του μαθηματικού αυτού προβλήματος εμφανίστηκε για πρώτη φορά το 1848, ως το πρόβλημα των 8 βασιλισσών και σωστή απάντηση δόθηκε ύστερα από λίγα χρόνια, χωρίς φυσικά τη χρήση υπολογιστών.
Το 1869 δόθηκε και η γενική μορφή του προβλήματος (n-queens) το οποίο έμεινε αναπάντητο για πολλές δεκαετίες έχοντας πονοκεφαλιάσει μαθηματικούς, πληροφορικούς και σκακιστές, αφού κανείς δεν είχε καταφέρει να βρει έναν αλγόριθμο που να τον λύνει εύκολα και αποτελεσματικά.
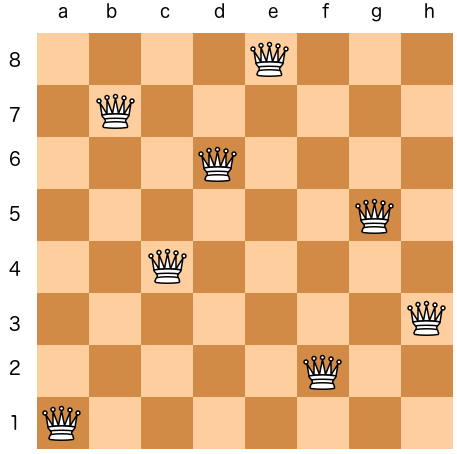
To σκακιστικό πρόβλημα “οι 8 βασίλισσες” (Πηγή: Θανάσης Κοπάδης)
Βρετανοί ερευνητές μάλιστα, πριν από λίγα χρόνια είχαν πει ότι κανένας υπολογιστής δεν θα τα καταφέρει ποτέ, προσφέροντας αμοιβή 1.000.000 δολάρια σε όποιον αποδείξει ότι κάνουν λάθος!
Όλα αυτά μέχρι πριν λίγο καιρό, όταν ο Michael Simkin, μαθηματικός στο Κέντρο Επιστημών και Ερευνών στο Harvand, έδωσε μια σχεδόν οριστική απάντηση. Υπολόγισε ότι υπάρχουν (0,143n)n τρόποι να τοποθετηθούν οι βασίλισσες, ώστε καμία να μην επιτίθεται στην άλλη σε γιγάντιες σκακιέρες nxn. Αν για παράδειγμα έχουμε 1.000.000 βασίλισσες, ο τύπος αυτός δίνει μια τελική απάντηση με 5 εκατομμύρια ψηφία.
Η λύση στο πρόβλημα δόθηκε εφαρμόζοντας μαθηματικές τεχνικές, αλγόριθμους, προβλήματα βελτιστοποίησης κ.α. και παρόλο που θεωρητικά είναι δυνατόν να πλησιάσουμε σε μια ακόμα πιο ακριβή απάντηση, η πολυετής αυτή εργασία αποδείχτηκε για τον ίδιο τον Simkin και την ομάδα του μια πραγματική δοκιμασία υπομονής και ανθεκτικότητας, πράγμα που τον ανάγκασε να δηλώσει ότι:
“Πιστεύω ότι πρέπει να τελειώσω με αυτό το πρόβλημα, όχι επειδή δεν έχω κάτι άλλο να κάνω με αυτό, αλλά επειδή ονειρευόμουν το σκάκι για χρόνια και πρέπει πλέον να προχωρήσω με τη ζωή μου και σε άλλα πράγματα.”
Η ψυχροπολεμική αναμέτρηση στο σκάκι που έμεινε στην ιστορία. Κάρποφ εναντίον Κορτσνόι. Επιστράτευσαν υπνωτιστές, γιόγκι και ψυχολόγους για τον τίτλο του παγκόσμιου πρωταθλητή
Ακολουθήστε την mixanitouxronou.gr στο Google News και μάθετε πρώτοι όλες τις ειδήσεις
Διαβάστε τις σημαντικότερες Ειδήσεις από την Ελλάδα και τον Κόσμο, στη mixanitouxronou.gr
